路径点优化

发表于 更新于 分类于 Changyan：
本文字数： 5.5k 阅读时长 ≈ 5 分钟

本文介绍路径点的优化方式，或者叫做多线段优化、轨迹点优化

根据设定阈值，去掉路径点中的部分多余点，以达到方便传输的目的

本文用UE4蓝图和C++蓝图函数库的2个方式解释

注:多种方法可以叠加使用

本算法提供了基于UE4的Demo，PC，安卓

GitHub工程下载

Demo演示动图

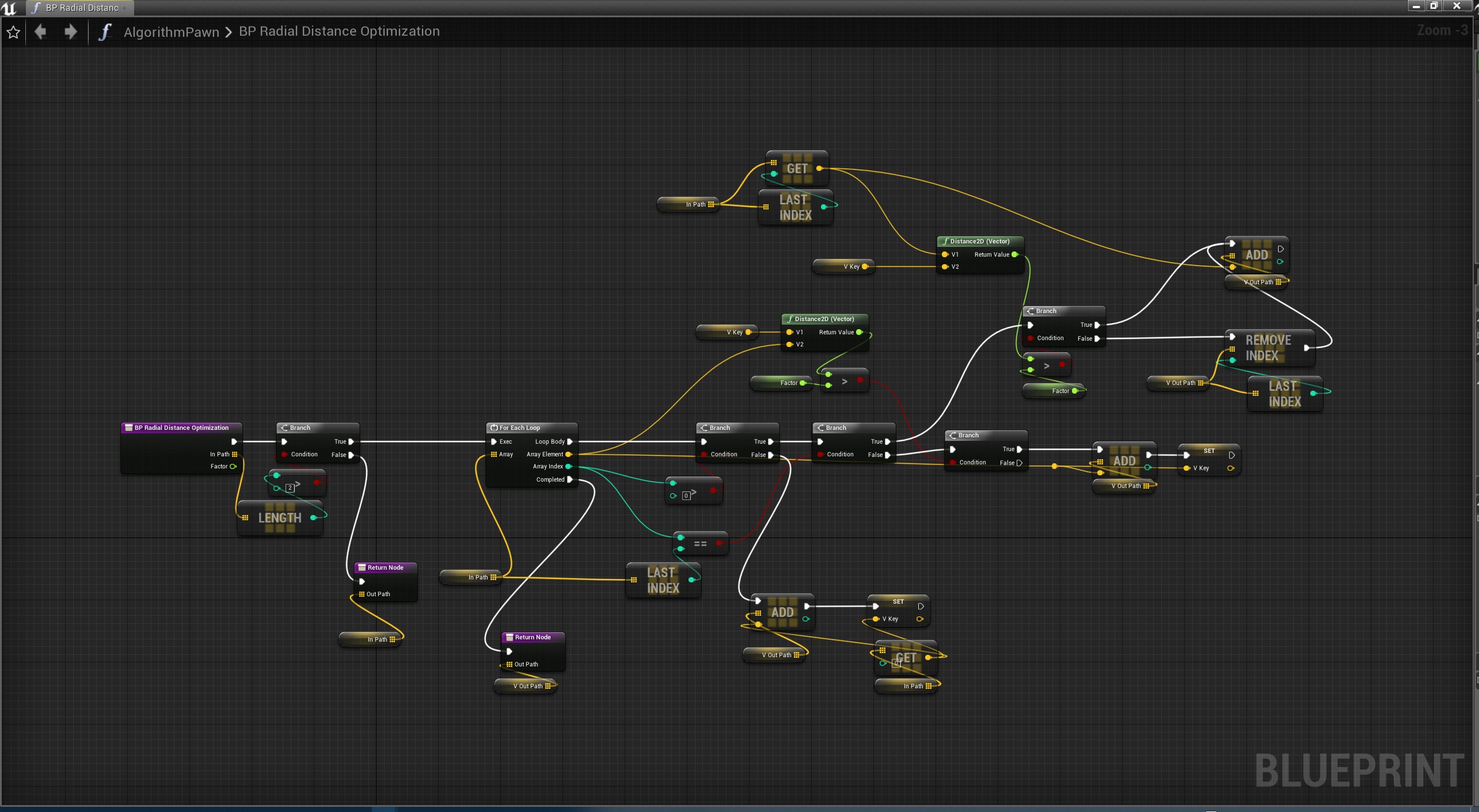
径向距离算法

又称为临近点优化，比较暴力的算法，效率高，精准度尚可

目的：去掉太接近的点

如果路径点中的相邻两点的距离小于设定的阈值，则舍去其中一个点。首先，以笔迹中的第一个点为基准点，计算第二个点与第一个点之间的距离，如果此距离小于给定的阈值，则舍去第二个点；如果此距离大于给定的阈值，则保留第二个点，并以其为新的基准点。然后再拿第三个点来与基准点判断距离，如此向后循环。

先贴代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//.h
//径向距离优化，小于distance的点会被优化
	UFUNCTION(BlueprintCallable,Category="UFlibAlgorithm|PathPointOptimization")
		static bool RadialDistanceOptimization(const TArray<FVector>& InPath,TArray<FVector>& OutPath, float Distance=50);
//.cpp
bool UFlibAlgorithm::RadialDistanceOptimization(const TArray<FVector>& InPath,  TArray<FVector>& OutPath, float Distance)
{
	if (InPath.Num()<3)
	{
		OutPath = InPath;
		return false;
	}
	FVector vKey= InPath[0];
	OutPath.Add(vKey);
	for (int32 i=1;i< InPath.Num()-1;i++)
	{
		if ((vKey- InPath[i]).Size()> Distance)
		{
			OutPath.Add(InPath[i]);
			vKey = InPath[i];
		}
	}
	if ((InPath.Last()-vKey).Size()<=Distance)//处理最后一个点
	{
		OutPath.Pop();
	}
	OutPath.Add(InPath.Last());
	return true;
}

蓝图

曲率算法

去除大于设定曲率阈值的角度的点

目的：去除角度偏移过大的线段

设定3个点：p1,p2,p3

方向向量：前置向量v1=p2-p1,后置向量v2=p3-p2

v1和v2的夹角angle即我们需要与阈值比较的角度，如果大于阈值，那么点p2就不满足条件而被移除

这里带来了一个问题，即移除了p2以后，下一次计算的时候后置向量v2保持不变即当前点指向下一个点；但是前置向量怎么选择是一个问题，所以我们分别用了T124,T134,T234来分别3种计算方式，3种方式取前置向量的方式分别是

  • T124：前置向量v1=p2-p1，即保持原样
  • T134：v1=p3-p1，即跳过被移除点
  • T234：v1=p3-p2，即跟后置向量保持统一节奏

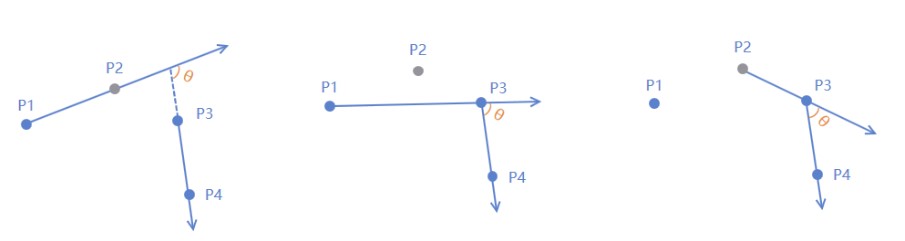
三种方式计算方式大同小异，下面先贴代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//.h
UENUM(BlueprintType)
enum class ECurvatureType:uint8
{
	T124,
	T134,
	T234
};

//曲率优化，大于角度angle的点会被优化，分为3个模式，推荐使用T134
UFUNCTION(BlueprintCallable, Category = "UFlibAlgorithm|PathPointOptimization")
	static bool CurvatureOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, ECurvatureType type=ECurvatureType::T134, float Angle = 90);

//.cpp
bool UFlibAlgorithm::CurvatureOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, ECurvatureType type, float Angle /*= 90*/)
{
	if (InPath.Num() < 3)
	{
		OutPath = InPath;
		return false;
	}
	FVector p1 = InPath[0];
	OutPath.Add(p1);
	FVector p2, p3, dirFWD, dirBWD;
	bool b124Found = true;
	for (int32 i=1;i<InPath.Num()-1;i++)
	{
		p2 = InPath[i];
		p3 = InPath[i + 1];
		if (b124Found||type!=ECurvatureType::T124)
		{
			dirFWD = p2 - p1;
		}
		dirBWD = p3 - p2;
		if (AngleBetween(dirBWD, dirFWD) <= Angle)
		{
			OutPath.Add(p2);
			p1 = p2;
			b124Found = true;
		}
		else
		{
			b124Found = false;
			if (type==ECurvatureType::T234)
			{
				p1 = p2;
			}
		}
	
		
	}
	OutPath.Add(InPath.Last());
	return true;
}
1
2
3
4
5
6
7
8
float UFlibAlgorithm::AngleBetween(FVector A, FVector B)
{
	A.Normalize();
	B.Normalize();
	return UKismetMathLibrary::DegAcos(UKismetMathLibrary::Dot_VectorVector(A, B));
	
}

蓝图

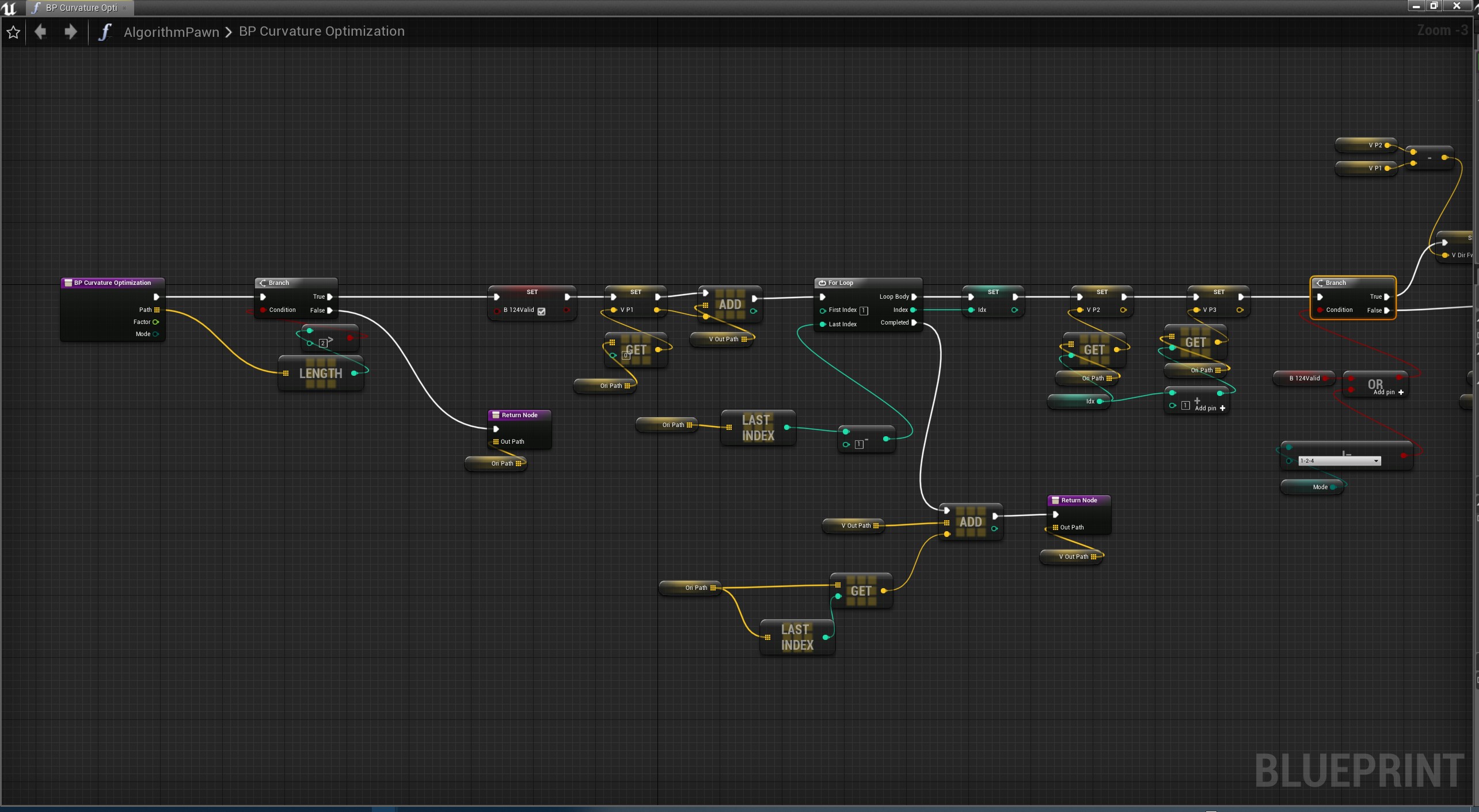
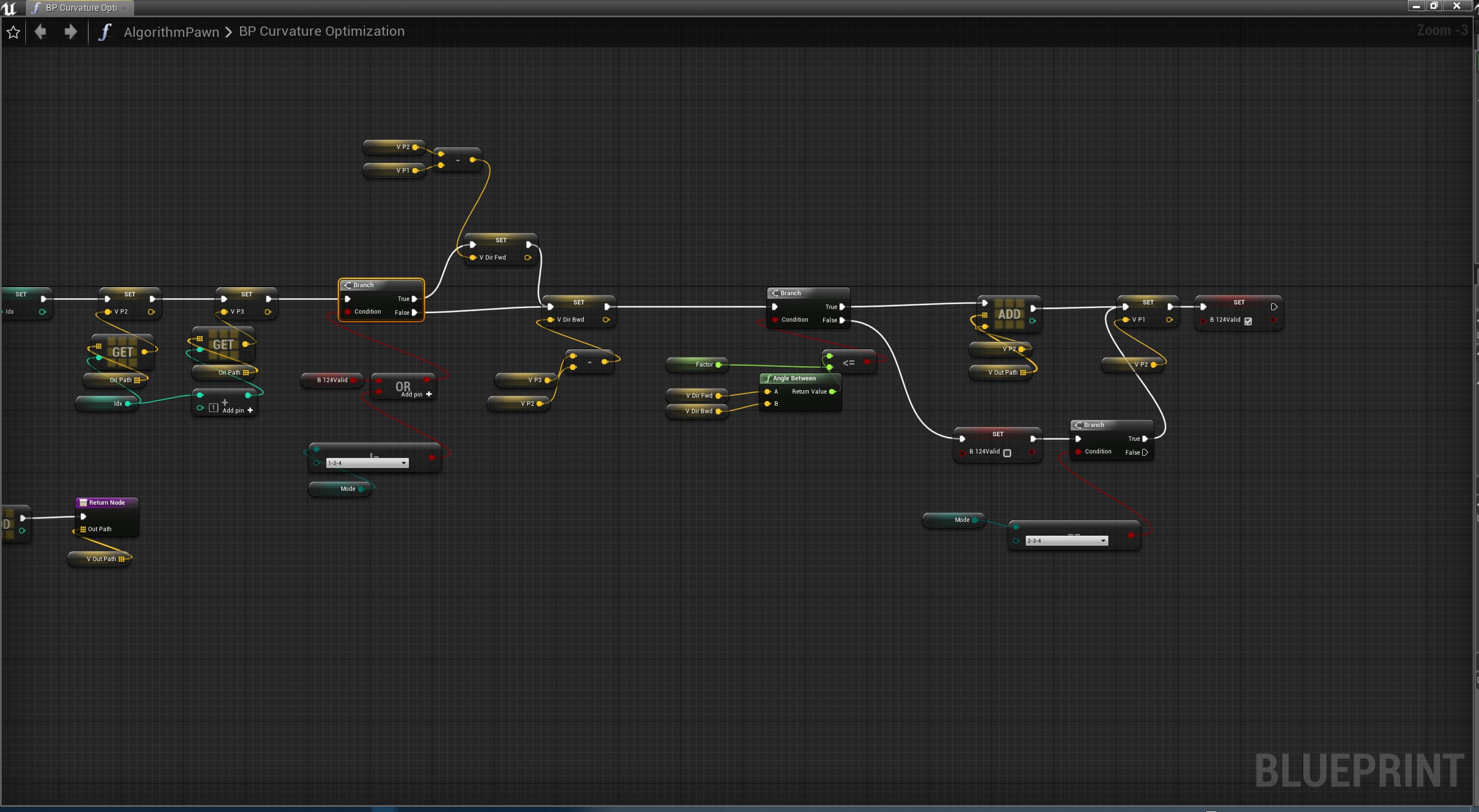
从结果测试发现，效果 T134>T124>T234

垂直距离算法

将点-线段的距离作为误差判据。对于每个顶点p，需要计算它与线段[p-1， p+1]的垂直距离，距离比给定误差小的点都将被移除。

目的:去除垂直距离偏移过大的点

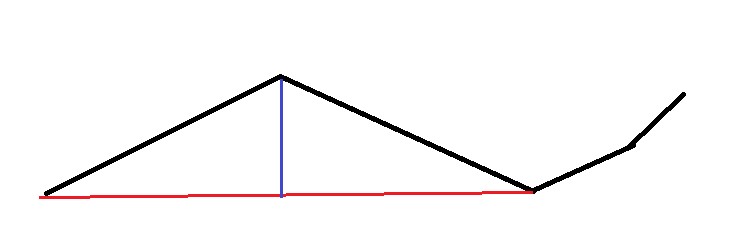
如图，如果蓝色线段即垂直距离大于设定阈值，则左右两天线段会被优化成红色线段

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//.h
//垂直距离优化，大于distance的点会被优化
UFUNCTION(BlueprintCallable, Category = "UFlibAlgorithm|PathPointOptimization")
	static bool PerpendicularDistanceOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, float Distance = 50);

//.cpp
bool UFlibAlgorithm::PerpendicularDistanceOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, float Distance /*= 50*/)
{
	if (InPath.Num() < 3)
	{
		OutPath = InPath;
		return false;
	}
	FVector vKey = InPath[0];
	OutPath.Add(vKey);
	FVector p1, p2, p3;
	p1 = InPath[0];
	for (int32 i=1;i<InPath.Num()-1;i++)
	{
		p2 = InPath[i];
		p3 = InPath[i + 1];
		float dis = UKismetMathLibrary::GetPointDistanceToLine(p2, p1, p3 - p1);
		if (dis<=Distance)
		{
			OutPath.Add(p2);
			p1 = p2;
		}
	}
	OutPath.Add(InPath.Last());
	return true;

}

蓝图

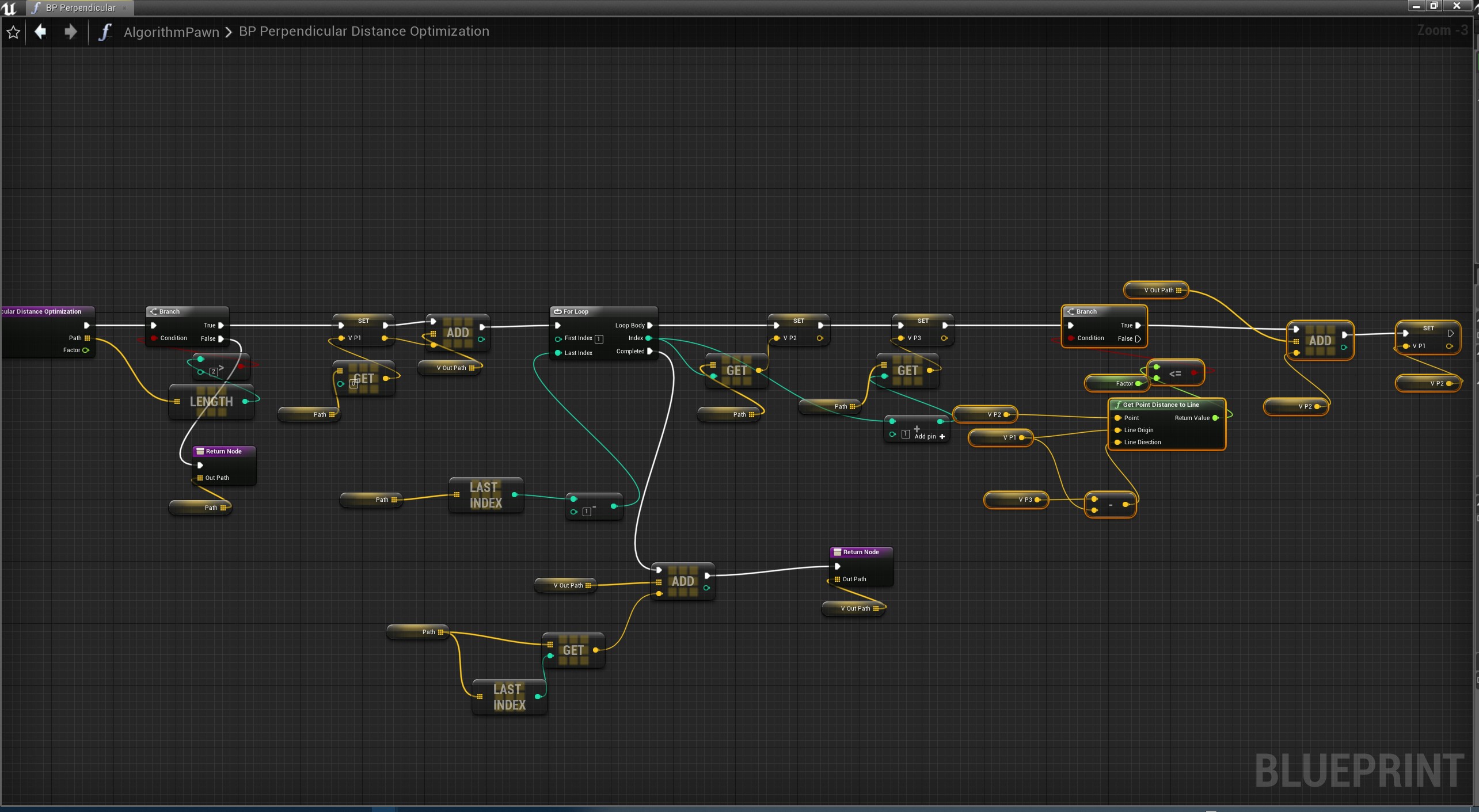
其实参考曲率优化方式，这个方式也可以考虑3种前置向量即本代码中p1的选择问题，本代码种应该是类似T234的方式，有兴趣的可以自己尝试其他几个方式

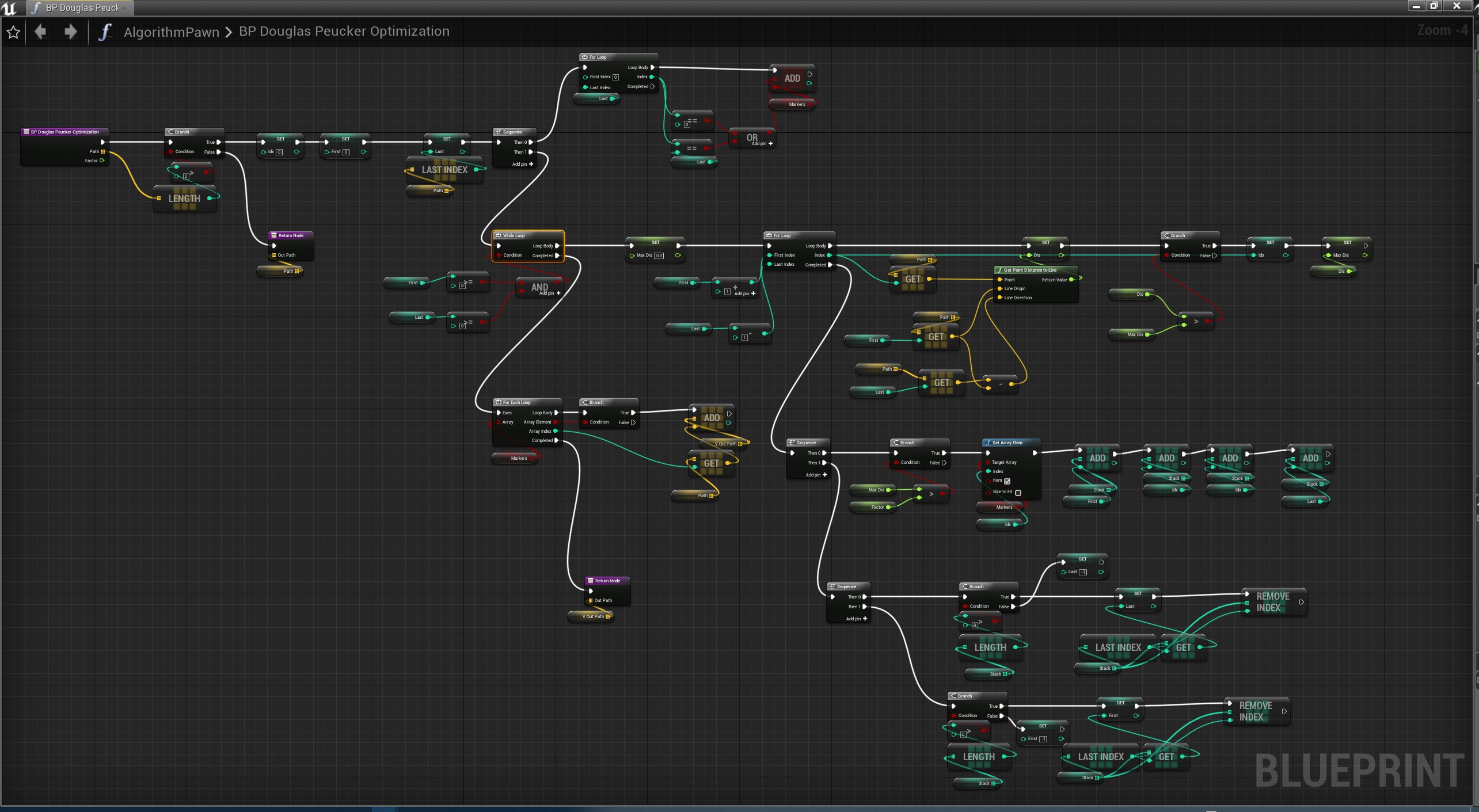
道格拉斯-普克算法

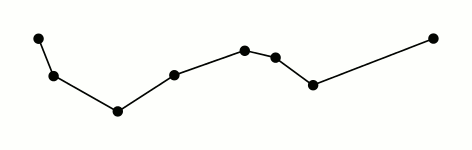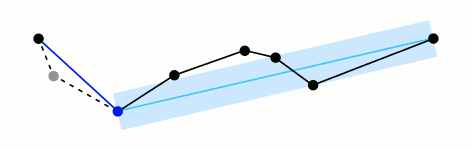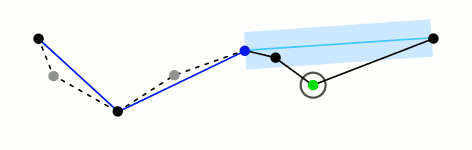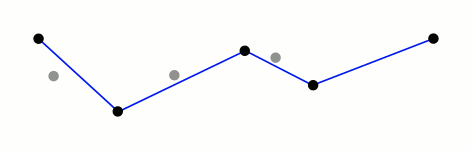
一种迭代适应点算法，它将曲线近似表示为一系列点，并减少点的数量。

算法的基本思路是：对每一条曲线的首末点虚连一条直线，求所有点与直线的距离，并找出最大距离值 dmax ，用 dmax 与阈值 D 相比。若 dmax < D ，这条曲线上的中间点全部舍去；若 dmax ≥ D ，则保留 dmax 对应的坐标点，并以该点为界，把曲线分为两部分，对这两部分循环使用该方法。
此算法在时间复杂度和空间复杂度要明显高于其它两种，但是它的效果较好

先来一个动图

贴代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
//.h
/*
	达格拉斯多普优化，使用迭代计算
	效率相对低但是精度高
	*/
UFUNCTION(BlueprintCallable, Category = "UFlibAlgorithm|PathPointOptimization")
	static bool DouglasPeuckerOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, float Distance = 50);


//.cpp
bool UFlibAlgorithm::DouglasPeuckerOptimization(const TArray<FVector>& InPath, TArray<FVector>& OutPath, float Distance /*= 50*/)
{

	if (InPath.Num() < 3)
	{
		OutPath = InPath;
		return false;
	}
	int32 idx, first, last;
	first = idx = 0;
	last = InPath.Num() - 1;
	TArray<bool> Markers;
	Markers.AddUninitialized(last + 1);
	Markers[0] = true;
	Markers.Last() = true;
	float maxDis = 0;
	TArray<int32> stack;
	while (first>=0 && last>=0)
	{
		maxDis = 0;
		for (int32 i=first+1;i<last;i++)
		{
			float dis = UKismetMathLibrary::GetPointDistanceToLine(InPath[i], InPath[first], InPath[last] - InPath[first]);
			if (dis>maxDis)
			{
				idx = i;
				maxDis = dis;
			}
		}
		if (maxDis>Distance)
		{
			Markers[idx] = true;
			stack.Add(first);
			stack.Add(idx);
			stack.Add(idx);
			stack.Add(last);
		}
		if (stack.Num()>0)
		{
			last = stack.Pop();
		}
		else
		{
			last = -1;
		}
		if (stack.Num() > 0)
		{
			first = stack.Pop();
		}
		else
		{
			first = -1;
		}

	}

	for (int32 i=0;i<Markers.Num();i++)
	{
		if (Markers[i])
		{
			OutPath.Add(InPath[i]);
		}
	}
	return true;



}

蓝图