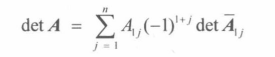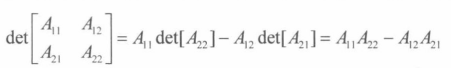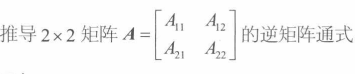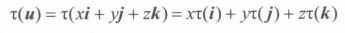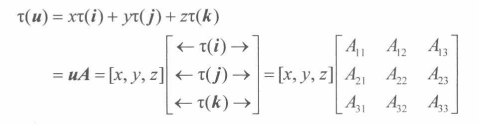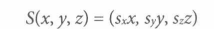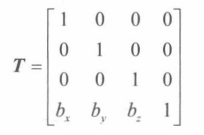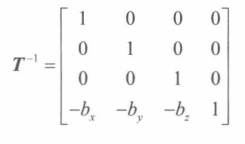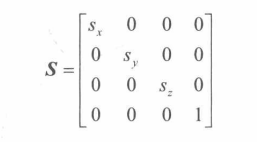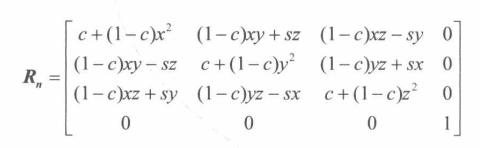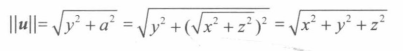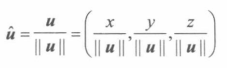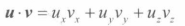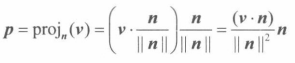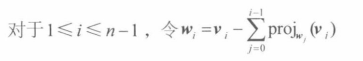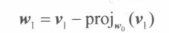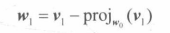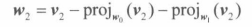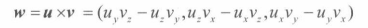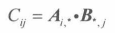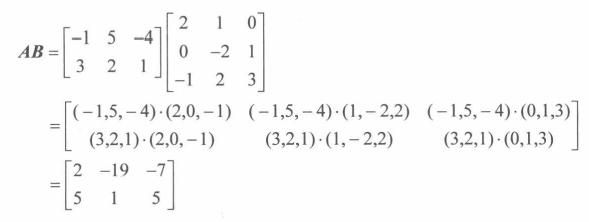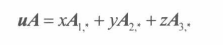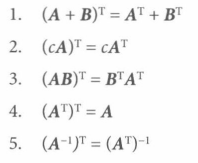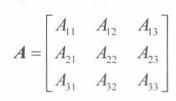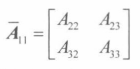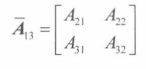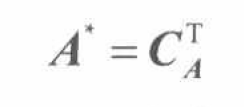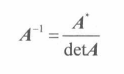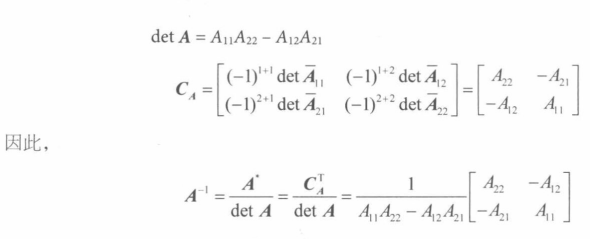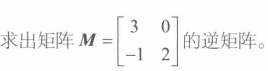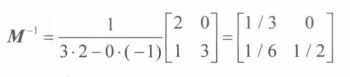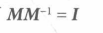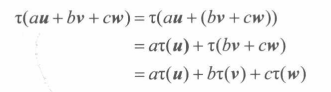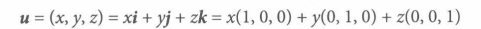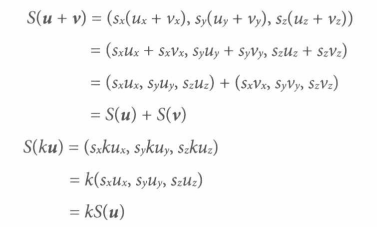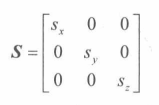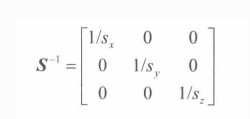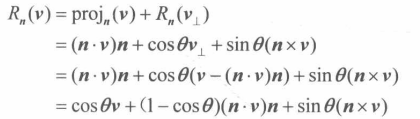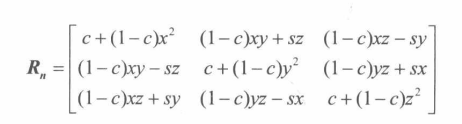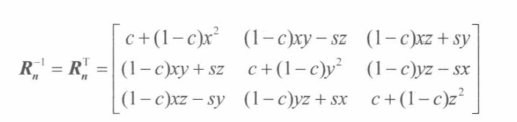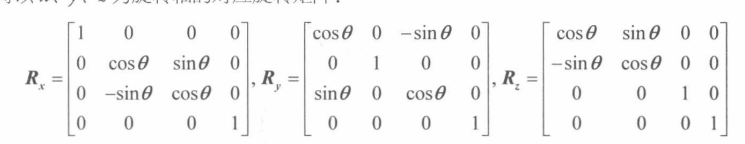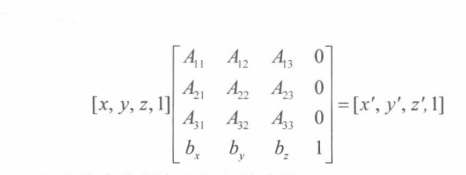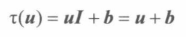向量代数 向量 DirectX3D采用的左手坐标系
左手坐标系:伸出左手,手指方向对准X轴正方向,弯曲手指对象Y轴正方向,大拇指指的就是Z轴正方向
向量的基本运算
向量加法的几何意义u+v,即u的尾部与v的头部重合
向量的长度和单位向量
3D向量的模可以用2次毕达哥拉斯定理(勾股定理)计算得到
一个向量的长度变为单位长度称为向量的规范化(normalizing) ,具体实现方法是
点积
点积(dot product)是一种计算结果为标量值的向量乘法
如果u·v=0,那么u和v正交(垂直)
如果u·v>0,那么夹角为锐角,即小于90°
如果>0,那么夹角为钝角
正交投影
即向量p是v在n向量上的投影
一般的投影公式如下
正交化 如果向量集里面所有向量都相互正交,那么此向量集是规范正交
格拉姆-施密特正交化
从文字上描述即,将向量v添加到规范正交集中时,需要用v减去这个规范正交集中的所有其他向量{w1,w2…}方向上的分量投影 ,这样确保新加入的v与该集合中的其他放量相互正交
假设有向量集{v0,v1},将其规范正交至集{w0,w1}
则需要进行如下操作
如果是三维向量集{v0,v1,v2},至规范正交集{w0,w1,w2}
则进行如下操作
叉积 叉积公式
两个向量叉积的意义即得到正交于两个向量的向量,采用的左手坐标系,即手指指向一个向量,通过向内弯曲小于等于180°的角度后到达另外一个向量,则大拇指方向是叉积所得向量的方向
用叉积类规范正交化
点 点(x,y,z)即从原点至该点的向量
用DirectXMath库 DirectXMath变量的使用规范
局部变量或全局变量用XMVECTOR类型
对于类中的数据成员,用XMFLOAT2\XMFLOAT3和XMFLOAT4类型
在运算之前,通过加载函数将XMFLOATn类型转换成XMVECTOR类型
用XMVECTOR实例来进行运算
通过存储函数将XMVECTOR类型转换为XMFLOATn类型
加载方法和存储方法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 XMVECTOR XM_CALLCONV XMLoadFloat2 (const XMFLOAT2* pSource) ;XMVECTOR XM_CALLCONV XMLoadFloat3 (const XMFLOAT3* pSource) ;void XM_CALLCONV XMStoreFloat2 (XMFLOAT2* pDestination,FXMVECTOR V) float XM_CALLCONV XMVectorGetX (FXMVECTOR V) float XM_CALLCONV XMVectorGetY (FXMVECTOR V) float XM_CALLCONV XMVectorGetZ (FXMVECTOR V) float XM_CALLCONV XMVectorGetX (FXMVECTOR V) XMVECTOR XM_CALLCONV XMVectorSetX (FXMVECTOR V,float x) ;XMVECTOR XM_CALLCONV XMVectorSetY (FXMVECTOR V,float y) ;XMVECTOR XM_CALLCONV XMVectorSetZ (FXMVECTOR V,float z) ;.XMVECTOR XM_CALLCONV XMVectorSetW (FXMVECTOR V,float w) ;
参数传递 传递规则
前三个 XMVECTOR 参数用类型 FXMVECTOR
第四个 XMVECTOR 参数用 GXMVECTOR
第5、6个 XMVECTOR 参数用 HXMVECTOR
其余的 XMVECTOR 参数用 CXMVECTOR
在32位windows系统,编译器将根据**_fastcall**调用约定将前3个XMVECTOR参数传递到寄存器,其余放到栈
在32位windows系统,编译器将根据**_vectorcall**调用约定将前6个XMVECTOR参数传递到寄存器,其余放到栈上
其余平台上的定义,可以参见 DirectXMath库文档中的 Library Internals下的 Calling Converntions 部分的[DirectXMath]
常向量 XMVECTOR类型的常量实例用 XMVECTORF32
1 static const XMVECTORF32 v1 = { 0.5f ,1.0f ,1.0f ,1.0f };
XMVECTORF32是一种16字节对齐的结构体,数学库中有将他转换至XMVECTOR类型的运算符
另外也可以用XMVECTORU32类型来创建由证书数据构成的XMVECTOR常向量
1 static const XMVECTORU32 v2 = { 1 ,2 ,3 ,4 };
重载运算符 XMVECTOR类型针对向量的加法、减法和标量乘法都重载了运算符,如下
其他 DirectXMath库定义了一组于PI有关的常用数学常量近似值
另外还有角度和弧度之间的转化以及比较大小的函数
Setter函数 DirectXMath库提供了下列函数,用来设置XMVECTOR类型中的数据
1 2 3 4 5 6 7 8 9 10 XMVECTOR XM_CALLCONV XMVectorZero () ;XMVECTOR XM_CALLCONV XMVectorSplatOne () ;XMVECTOR XM_CALLCONV XMVectorSet (float x,float y,float z,float w) ;XMVECTOR XM_CALLCONV XMVectorReplicate (float value) ;XMVECTOR XM_CALLCONV XMVectorSplateX (FXMVECTOR V) ;
使用案例 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 #include <DirectXMath.h> #include <DirectXPackedVector.h> #include <stdlib.h> #include <iostream> using namespace DirectX;using namespace DirectX::PackedVector;using namespace std;ostream& XM_CALLCONV operator <<(ostream& os, FXMVECTOR v) { XMFLOAT4 dest; XMStoreFloat4 (&dest, v); os << "(" << dest.x << "," << dest.y << "," << dest.z <<"," <<dest.w<< ")" << endl; return os; } int main () if (!XMVerifyCPUSupport ()) { cout << "directx math not supported" << endl; return 0 ; } static const XMVECTORF32 v1 = { 0.5f ,1.0f ,1.0f ,1.0f }; XMVECTOR v2 = XMVectorReplicate (0.99f ); XMVECTOR v3 = { .5 f,.5 f,.5 f,.5 f }; XMVECTOR v4 = XMVectorSet (1 , 2 , 3 , 4 ); XMVECTOR v5 = XMVectorSplatOne (); XMVECTOR v6 = XMVectorZero (); XMVECTOR v7 = XMVectorSplatZ (v4); cout << v1 << v2 << v3 << v4 << v5 << v6 << v7; system ("pause" ); return 0 ; }
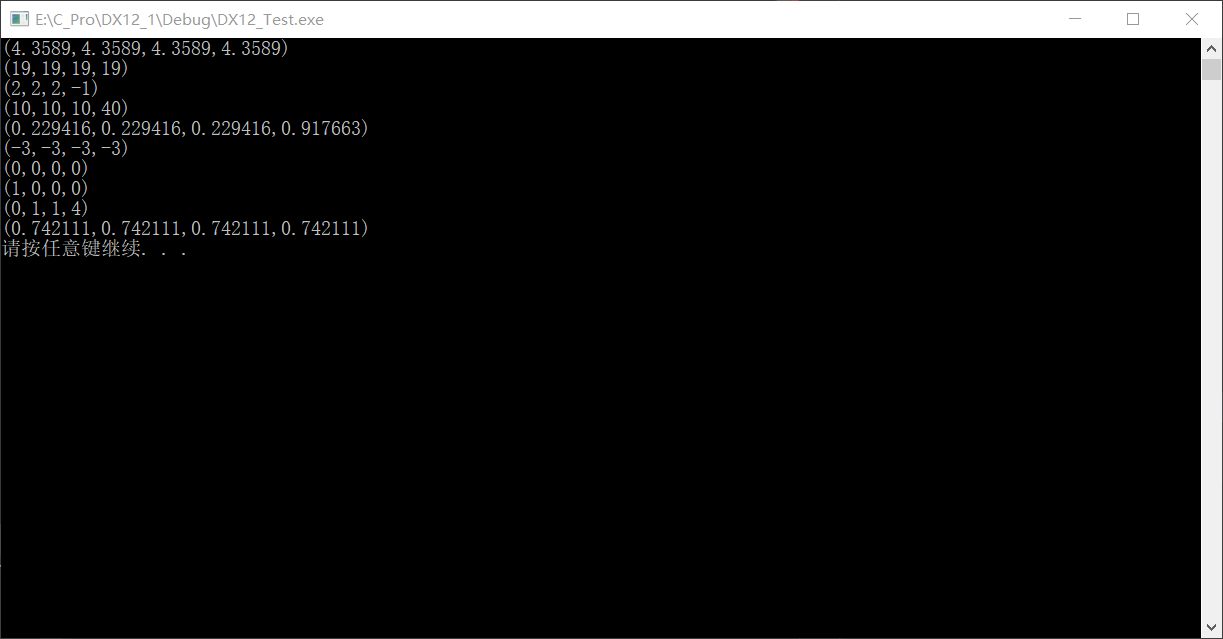
向量函数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 XMVECTOR v1 = XMVectorSet (1 , 1 , 1 , 4 ); XMVECTOR v2 = XMVectorSet (-1 , -1 , -1 , 5 ); XMVECTOR v3 = XMVectorSet (1 , 0 , 0 ,0 ); XMVECTOR a = XMVector4Length (v1); XMVECTOR b = XMVector4LengthSq (v1); XMVECTOR c = v1 - v2; XMVECTOR d = 10 * v1; XMVECTOR e = XMVector4Normalize (v1); XMVECTOR f = XMVector3Dot (v1,v2); XMVECTOR g = XMVector3Cross (v1, v2); XMVECTOR projw, perpw; XMVector3ComponentsFromNormal (&projw, &perpw, v1, v3); XMVECTOR angle = XMVector4AngleBetweenVectors (v1, v2); cout << a<<b<<c<<d<<e<<f<<g<<projw<<perpw<<angle;
浮点数的误差 1 2 XMVector Epsilon={0.1 ,0.1 ,0.1 ,0.1 }; bool IsEqual = XMVectorNearEqual (v1, v2,Epsilon);
矩阵代数 定义 m*n的矩阵M,即由m行,n列构成的矩形阵列
乘法
矩阵AxB 乘法的前提条件:A的列数必须于B的行数相同
乘法公式
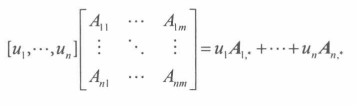
向量于矩阵乘法
转置矩阵 转置矩阵(transpose matrix) 是将原矩阵阵列的 行与列进行互换 即mn的矩阵变成nm的矩阵
**M **的转置矩阵记作 Mt
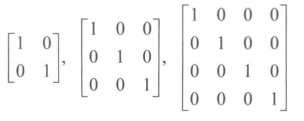
单位矩阵 单位矩阵(identity matrix)是一种主对角线上的元素都是 1 ,其他元素都是0的方阵,如
任何单位与单位矩阵相乘,得到的依然是原来的矩阵,而且满足交换律
MI=IM=M
矩阵的行列式 行列式记作: det A
余子阵 n x n的矩阵A,余子阵(minor matrix) i 行和第 j 列的**(n-1)*(n-1)**矩阵
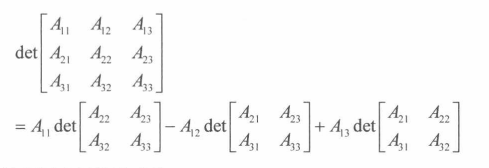
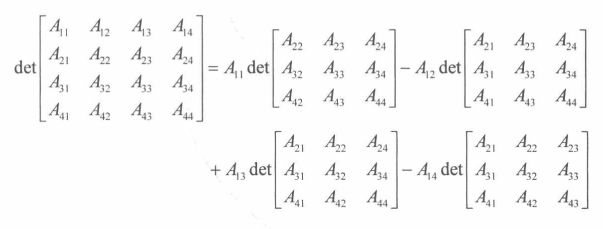
行列式
一个矩阵的行列式就是一个平行多面体的(定向的)体积,这个多面体的每条边对应着对应矩阵的列。如果学生得知了这个秘密(在纯粹的代数式的教育中,这个秘密被仔细的隐藏了起来),那么行列式的整个理论都将成为多重线性形式理论的一部分。倘若用别的方式来定义行列式,任何敏感的人都将会永远痛恨诸如行列式,Jacobian式,以及隐函数定理这些东西。
——俄国数学家阿诺尔德(Vladimir Arnold)《论数学教育》
伴随矩阵
如果A中的每个元素分别计算出Cij ,并将它至于矩阵CA 中的第 i 行,第 j 列,那么将获得矩阵A的 代数余子式矩阵(cofactor matrix of A)
取矩阵CA 的转置矩阵,得到矩阵A的伴随矩阵(adjoint matrix of A) ,记作
逆矩阵
只有方阵才有逆矩阵
n x n矩阵M的逆也是一个n x n的矩阵,记作 M-1
不是每个方阵都有逆矩阵,存在逆矩阵的方阵称为可逆矩阵(invertible matrix) ,不存在逆矩阵的叫做奇异矩阵(singular matrix)
可逆矩阵的逆矩阵是唯一的
可逆矩阵有逆矩阵相乘等到单位方阵: MM-1 =M-1 M=I,矩阵与其逆矩阵妈祖交换律
逆矩阵的推导公式
案例,
DirectXMath库处理矩阵阵列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 ostream& XM_CALLCONV operator <<(ostream& os, FXMVECTOR v) { XMFLOAT4 dest; XMStoreFloat4 (&dest, v); os << "(" << dest.x << "," << dest.y << "," << dest.z <<"," <<dest.w<< ")" ; return os; } ostream& XM_CALLCONV operator <<(ostream& os, FXMMATRIX v) { for (int i=0 ;i<4 ;i++) { os << XMVectorGetX (v.r[i]) << "\t" ; os << XMVectorGetY (v.r[i]) << "\t" ; os << XMVectorGetZ (v.r[i]) << "\t" ; os << XMVectorGetW (v.r[i]) << "\t" ; os << endl; } return os; } int main () if (!XMVerifyCPUSupport ()) { cout << "directx math not supported" << endl; return 0 ; } XMMATRIX A ( 1.0f , 0.0f , 0.0f , 0.0f , 0.0f , 2.0f , 0.0f , 0.0f , 0.0f , 0.0f , 4.0f , 0.0f , 1.0f , 2.0f , 3.0f , 1.0f ) XMMATRIX B = XMMatrixIdentity (); XMMATRIX C = A * B; XMMATRIX D = XMMatrixTranspose (A); XMVECTOR det = XMMatrixDeterminant (A); XMMATRIX E = XMMatrixInverse (&det, A); XMMATRIX F = A * E; cout << A << endl << B << endl << C << endl << D << endl << E << endl << det << endl << F; system ("pause" ); return 0 ; }
变换 线性变换 线性变换函数满足
线性变换函数公式
矩阵表示法 **u=(x,y,z)**也可以写作
矩阵表示法公式 R3 ,标准基向量 i=(1,0,0), j=(0,1,0), k=(0,0,1)
矩阵表示法公式2
根据线性组合,上述公式可以改写成
线性变换的矩阵表示法
我们称矩阵 A 是线性变换的矩阵表示法
缩放 定义
缩放变换的矩阵表达式
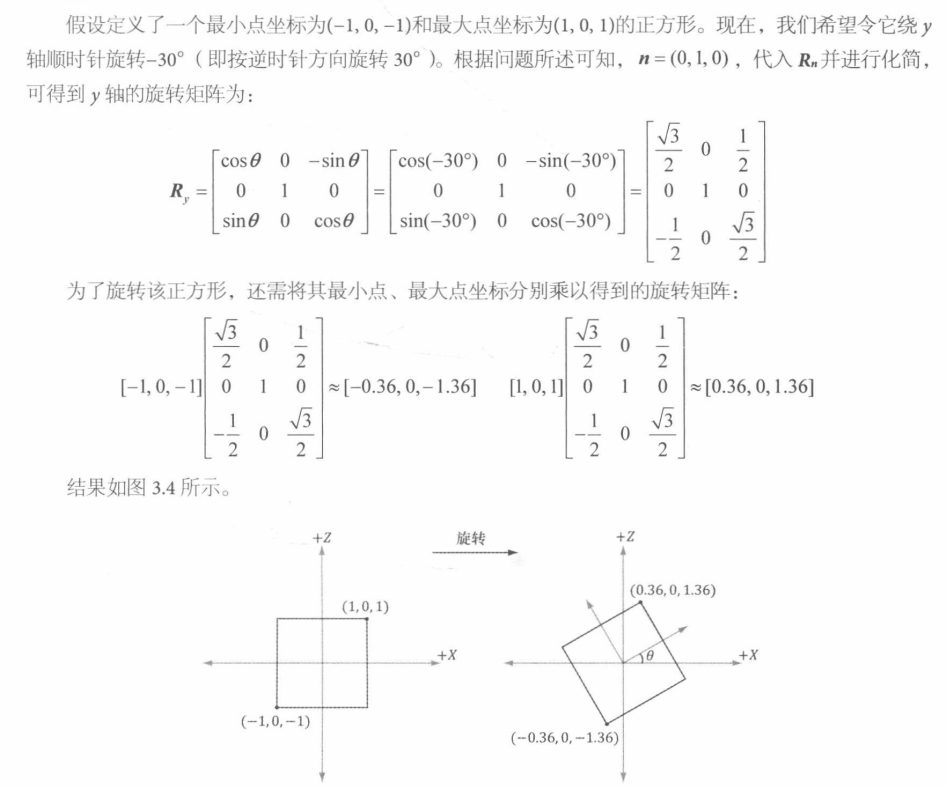
旋转 旋转矩阵基础公式
正交矩阵的逆矩阵
通俗公式 如果选择绕x、y、z n =(1,0,0)、n =(0,1,0)、n =(0,0,1)
案例
仿射变换 齐次坐标
(x,y,z,0) (x,y,z,1)
仿射变换定义
α(u)=τ(u)+b
如果w=1把坐标扩充为齐次坐标,那么把上述公式简化成
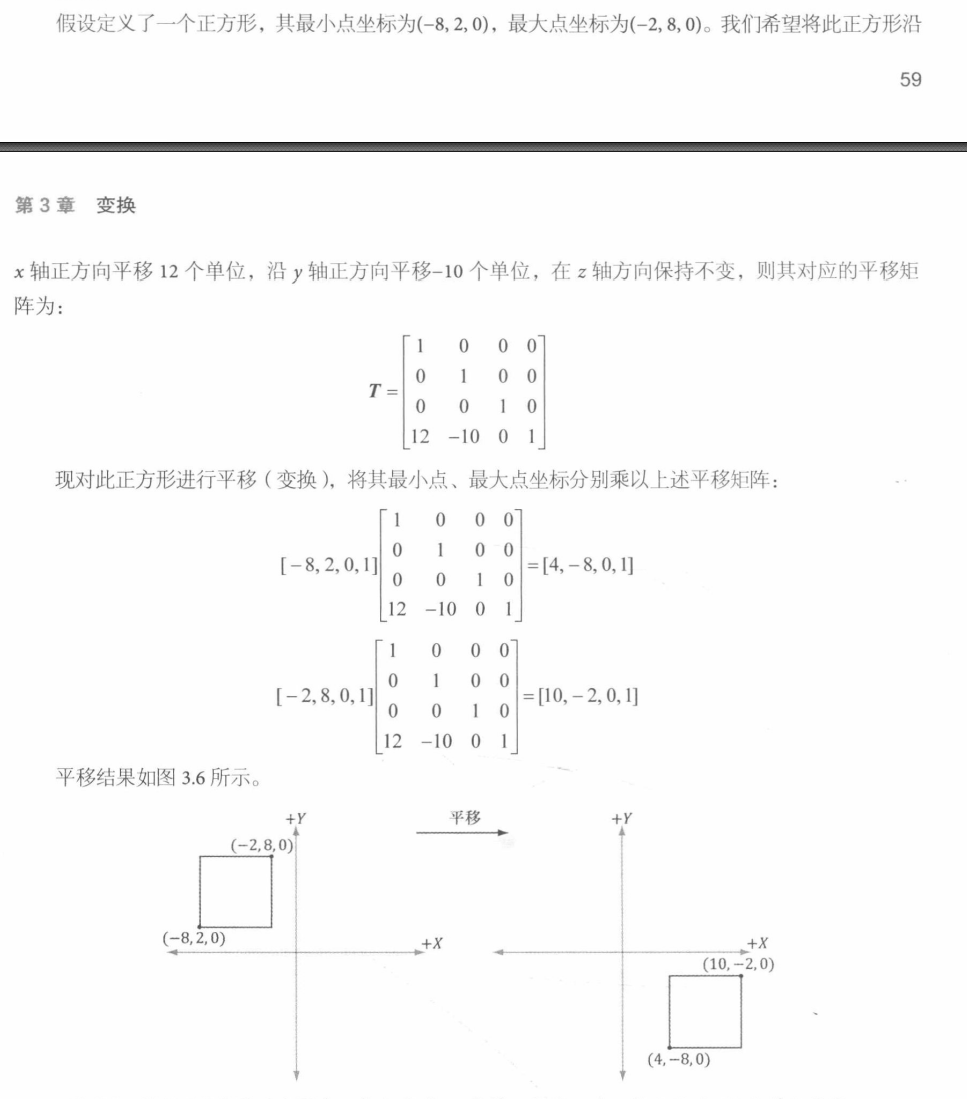
平移 恒等变换 恒等变换 是一种直接返回其输入参数的线性变换,如 I(u)=u
如果将平移变换定义为仿射变换,贼其中的线性变换就是一种恒等变换,即
平移矩阵
平移矩阵的逆矩阵
案例
缩放和旋转的放射矩阵
如果放射变换的 b=0 ,则放射变换就是线性变换
意味着,可以通过一个 4 x 4 的放射矩阵表达任意线性变换
4x4的缩放矩阵
4x4的旋转矩阵
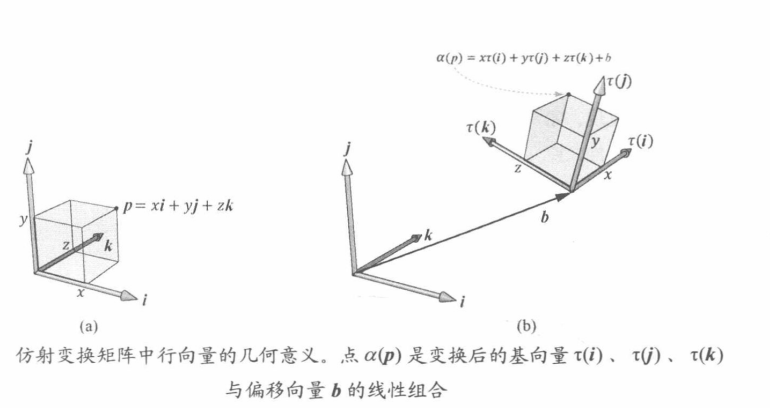
仿射变换矩阵的几何意义
变换的复合 假设S T R
因为矩阵乘法(不满足交换律),所以我么可以定义C=SRT
坐标变换 坐标变换矩阵/标架变换矩阵公式 结合律
3个标架F,G,H
A :F 转换到G 的变换矩阵B :G 转换到H 的变换矩阵pF F 中的一个向量求:此向量在标架H中的坐标PH
***(pF ***A)B =PH
(pG )B =PH
pF AB )=PH
逆矩阵 pF A PH
PF pH A-1
变换矩阵与坐标变换矩阵 在数学上,可以将改变几何体的变换 解释为坐标变换 ,反之亦然
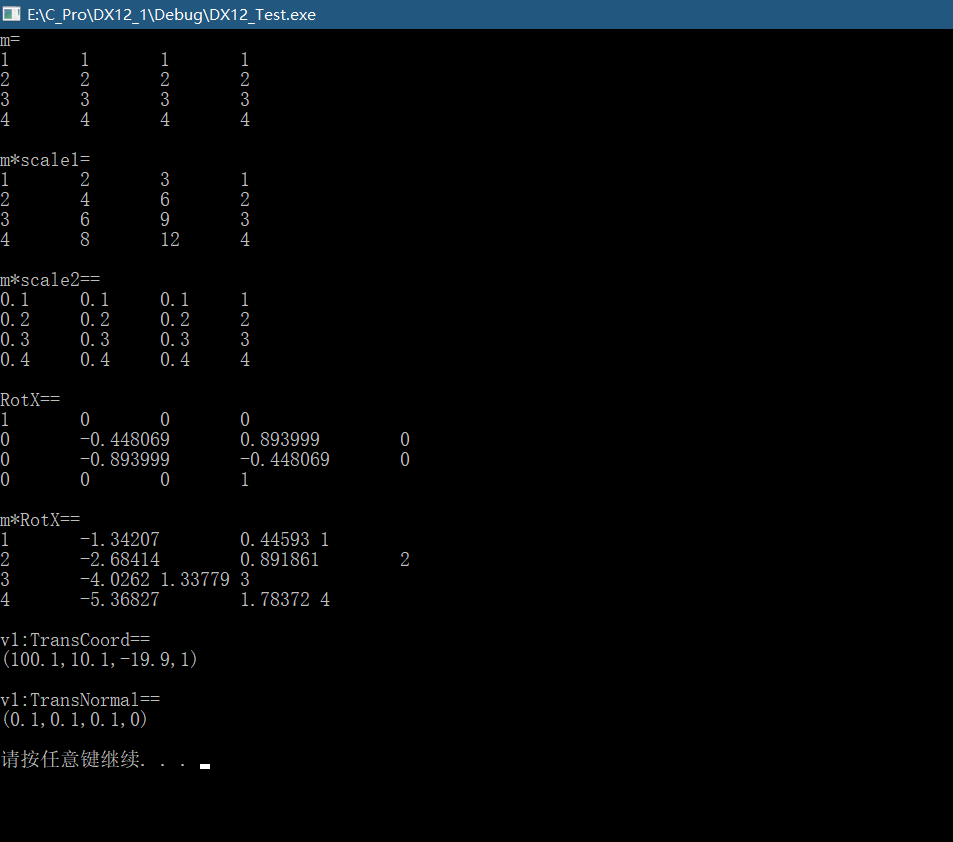
DirectXMath库的变换函数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 #pragma #include <windows.h> #include <iostream> #include <DirectXMath.h> #include <DirectXPackedVector.h> using namespace std;using namespace DirectX;using namespace DirectX::PackedVector;ostream& operator <<( ostream& os, FXMVECTOR v) { XMFLOAT4 value; XMStoreFloat4 (&value, v); os << "(" << value.x << "," << value.y << "," << value.z << "," << value.w << ")" << endl; return os; } ostream& operator <<(ostream& os, FXMMATRIX M) { for (int i=0 ;i<4 ;i++) { os << XMVectorGetX (M.r[i]) << "\t" ; os << XMVectorGetY (M.r[i]) << "\t" ; os << XMVectorGetZ (M.r[i]) << "\t" ; os << XMVectorGetW (M.r[i]) << "\t" ; os << endl; } return os; } int main () XMMATRIX m1 = { 1.0f , 1.0f , 1.0f , 1.0f , 2.0f , 2.0f , 2.0f , 2.0f , 3.0f , 3.0f , 3.0f , 3.0f , 4.0f , 4.0f , 4.0f , 4.0f }; XMMATRIX Scale1 = XMMatrixScaling (1.0f , 2.0f , 3.0f ); XMVECTOR v1 = XMVectorSet (0.1 , 0.1 , 0.1 , 0.1 ); XMMATRIX Scale2 = XMMatrixScalingFromVector (v1); XMMATRIX RotX = XMMatrixRotationX (90.f ); XMMATRIX RotY = XMMatrixRotationY (45.f ); XMMATRIX RotZ = XMMatrixRotationZ (-180.f ); XMVECTOR Axis= XMVectorSet (1 , 0 , 0 , 0 ); XMMATRIX RotAxis = XMMatrixRotationAxis (Axis, 45.f ); XMMATRIX TransT = XMMatrixTranslation (100.f , 10.f , -20.f ); XMVECTOR vTransCoord = XMVector3TransformCoord (v1, TransT); XMVECTOR vTransNormal = XMVector3TransformNormal (v1, TransT); cout << "m=" << endl << m1 << endl; cout << "m*scale1=" << endl<< m1* Scale1 << endl; cout << "m*scale2==" << endl << m1*Scale2 << endl; cout << "RotX==" << endl << RotX << endl; cout << "m*RotX==" << endl << m1 * RotX << endl; cout << "v1:TransCoord==" << endl << vTransCoord << endl; cout << "v1:TransNormal==" << endl << vTransNormal << endl; system ("pause" ); return 0 ; }

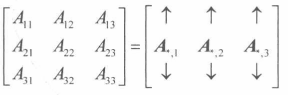
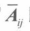 即从A中去除第 i 行和第 j 列的**(n-1)*(n-1)**矩阵
即从A中去除第 i 行和第 j 列的**(n-1)*(n-1)**矩阵