UE4中的数学随笔

发表于 2022-04-11 分类于 math 阅读次数： Changyan：

本文字数： 3.4k 阅读时长 ≈ 3 分钟

前言

记录UE开发时常用的数学方法

三角函数

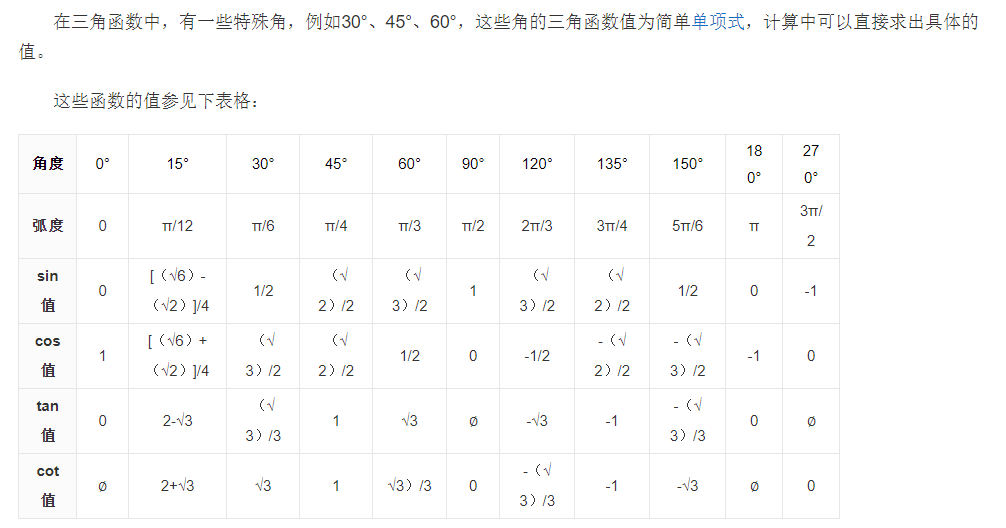
特殊角

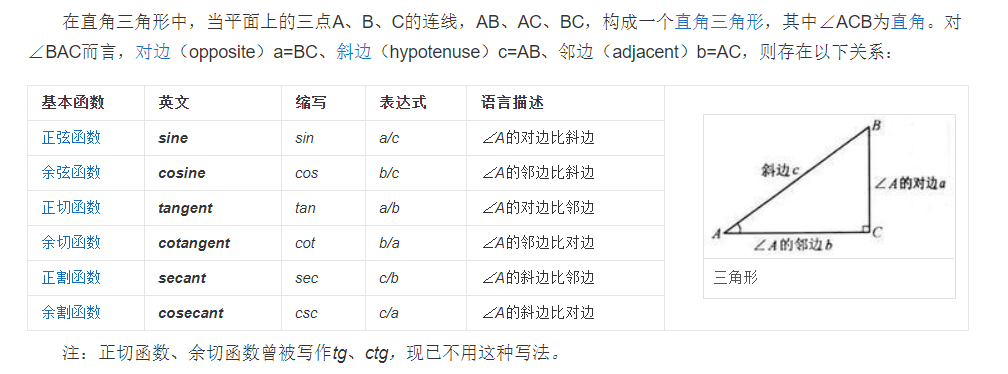
几何性质

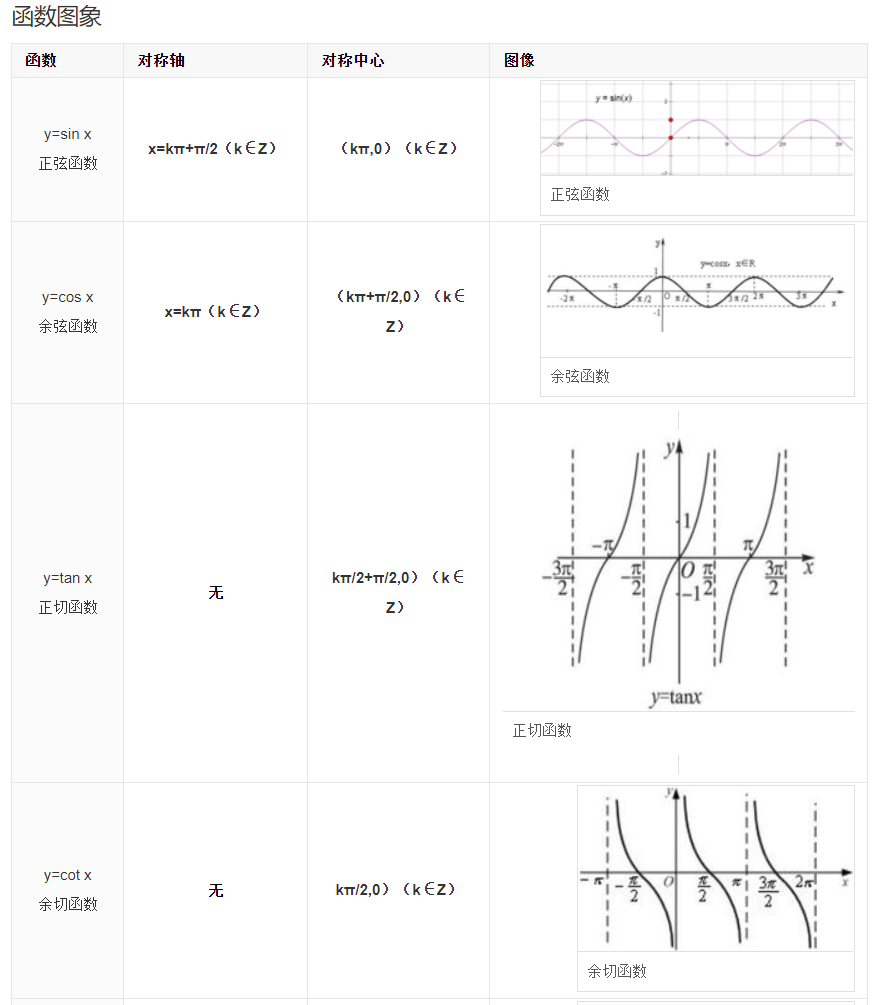
公式

公式1	公式2
sin（2kπ+α）=sin α	sin（π+α）=-sin α
cos（2kπ+α）=cos α	cos（π+α）=-cos α
tan（2kπ+α）=tan α	tan（π+α）=tan α
cot（2kπ+α）=cot α	cot（π+α）=cot α
sec（2kπ+α）=sec α	sec（π+α）=-sec α
csc（2kπ+α）=csc α	csc（π+α）=-csc α

公式3	公式4
sin（-α）=-sin α	sin（π-α）=sin α
cos（-α）=cos α	cos（π-α）=-cos α
tan（-α）=-tan α	tan（π-α）=-tan α
cot（-α）=-cot α	cot（π-α）=-cot α
sec（-α）=sec α	sec（π-α）=-sec α
csc（-α）=-csc α	csc（π-α）=csc α

UE4的三角函数

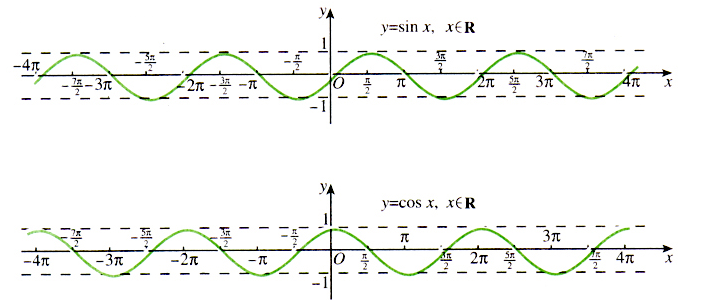
Radius就是用三角函数来计算，横轴是(0,kPI),纵轴是(0,1)
Degree就是用的基础的直角三角形函数,例如Sine是 Sinθ=a/c计算，输入参数是角度，得到的是[0,1]

Sine,ASine

蓝图Sine(Radius)

float UKismetMathLibrary::Sin(float A)
{
	return FMath::Sin(A);
}
float UKismetMathLibrary::Asin(float A)
{
	return FMath::Asin(A);
}

Sine(PI)–>0

Sine(PI/2)–>1

ASine(1)–>PI/2

ASine(-1)–>-PI/2

蓝图Sine(Degree)

float UKismetMathLibrary::DegSin(float A)
{
	return FMath::Sin(PI/(180.f) * A);
}
float UKismetMathLibrary::DegAsin(float A)
{
	return (180.f)/PI * FMath::Asin(A);
}

SineD(30)–>0.5

SineD(90)–>1

ASineD(0.5)–>30

ASineD(1)–>90

Cos,ACos

Cos(Radius)

Cos(PI)–>-1

ACos(1)–>0

ACos(-1)–>PI

Cos(Degree)

Cos(60)–>0.5

Cos(0)–>1

Tan

蓝图没有提供Cot方法，本质上就是tan的2个参数反转一下

特殊角度的值

Tan(PI)–>0

Tan(PI/2) –>垃圾值，如图

ATan(0)–>0

ATan(无穷)–>接近于PI/2,如图

TanD(45)–>1

TanD(90)–>垃圾值，因为分母=0

ATanD(1)–>45

ATanD(0)–>0

ATanD( 无穷大)–>接近于90

蓝图额外Tan方法

ATan2有2个方法，简单说就是提供了2个输入参数：A,B

计算就是A/B

ATan2D，可以输入2条边的长度，得到比例

三角函数应用

求两个向量夹角

1	cosx=ab/[\|a\|\|b\|]

float GetTwoVectorAngle(FVector a,FVector b)
{
    if (a.Size()==0||b.Size()==0)
	{
		return 0;
	}
	float cos = UKismetMathLibrary::Dot_VectorVector(a, b) / (a.Size()*b.Size());
	return UKismetMathLibrary::DegAcos(cos);
}

得到的是[-180,180]的值

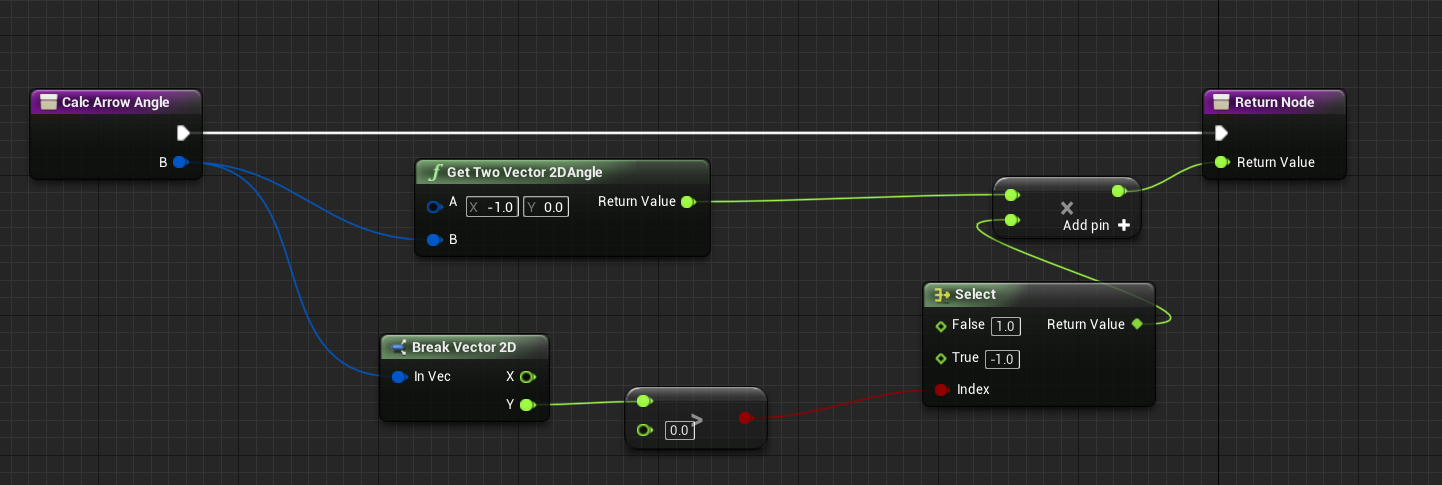
UMG中的箭头

由于UMG的旋转是[-180，180]的范围

所以可以对方向向量与(-1,0)做夹角计算，如下图得到旋转值

按角度旋转向量

已知点(x1,y1),绕(x2,y2)旋转θ

1 2	x= (x1 - x2)cos(θ) - (y1 - y2)sin(θ) + x2 ; y= (x1 - x2)sin(θ) + (y1 - y2)cos(θ) + y2 ;

如果是绕原点旋转，公式可以简化成

1 2	x= x1cos(θ) - y1sin(θ) ; y= x1sin(θ) + y1cos(θ) ;

在UE中已经封装了很多比较方便的库来旋转向量

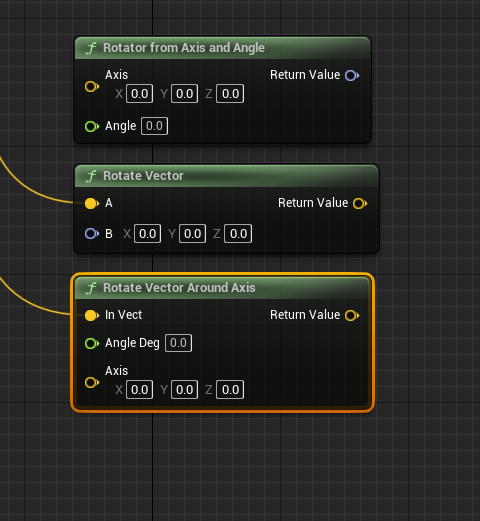
UE中的矩阵变换

相对关系

A相对于B的变换信息, 用TransformA.GetRelativeTransform(TransformB);

蓝图有两个类似的API, 但是有点容易造成歧义

我们看实现

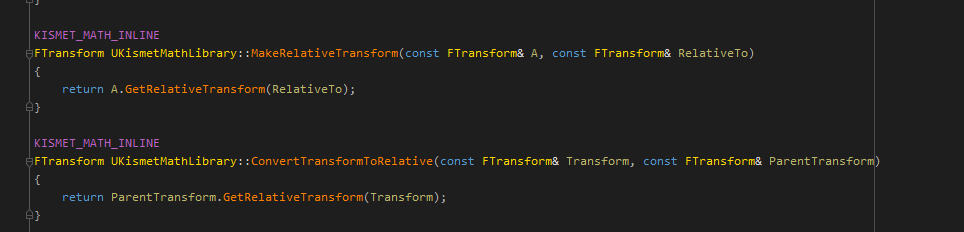
MakeRelativeTransform的第二个参数输入Parent这个没问题,

但是看ConvertTransformToRelative的第二个输入Parent获取到的实际上是夫相对于子的相对变换信息, 那么两者等价的情况要如下图所示

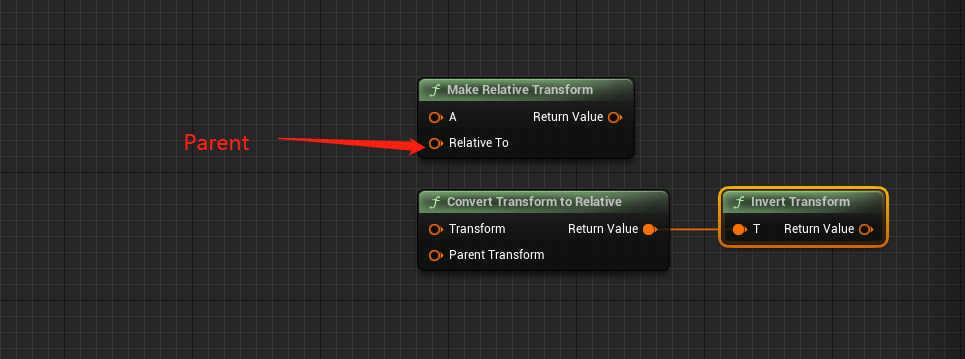
空间转换

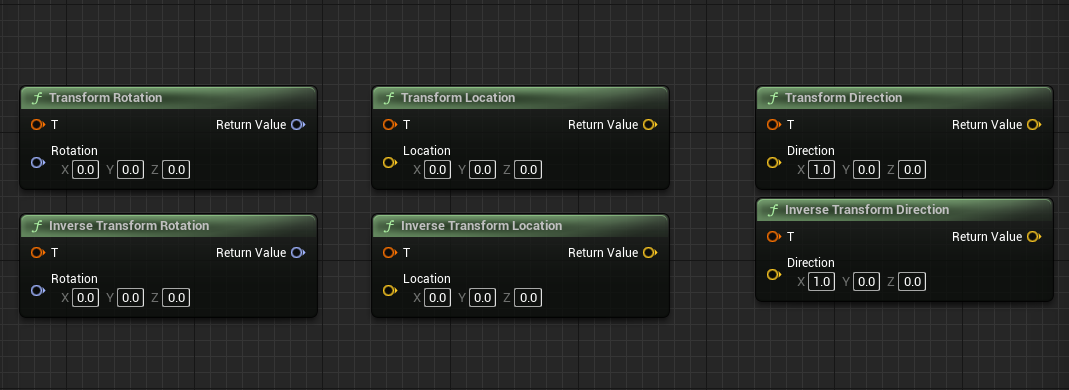
//把Location转换至T的空间，如果是GetActorTransform获取Transoform，即世界空间
T.TransformPosition(Location);
//相反, Location是T空间的相对位置,通过这个方法转换成T的世界空间
T.InverseTransformPosition(Location);

上面即Location的空间转换, 同理还有Direction和Rotation, 方法类似

蓝图只是套了一层,没有实质性区别

逆矩阵

1	T.Inverse();

矩阵乘法

c++中可以直接对Transofomr进行*运算符运算, 在蓝图中包了一层, 使用的是FTransform UKismetMathLibrary::ComposeTransforms(const FTransform& A, const FTransform& B)

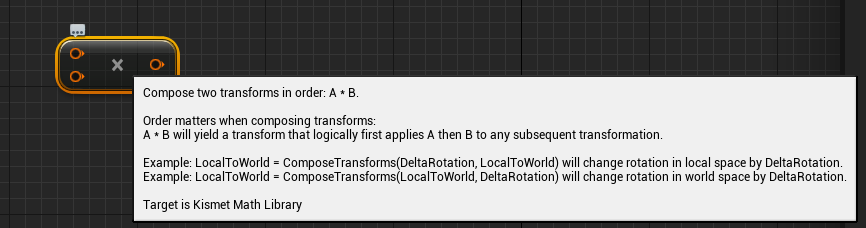
乘法需要区分左乘和右乘, 这个跟图形中常用的运算比较类似,ComposeTransforms注释中的用法是很多场合中会用到的

先通过一个案例了了解一下矩阵乘法

经常需要用到角色的RootMotion信息转换成角色世界空间的位移信息，这个如何做？

首先从动画提取RootMotion信息，这个有很多已有的API了，如

1	FTransform UAnimSequence::ExtractRootMotionFromRange(float StartTrackPosition, float EndTrackPosition) const;

提取出来的RootMotion数据（假设叫RM）是模型空间的，那么需要在世界空间进行这个偏移得到RMWS

1	RMWS = RM * MeshTransformWS;//模型世界空间变换信息进行rootmotion偏移

然后需要把RMWS数据通过逆矩阵转换到Character空间的，因为模型可能会有相对偏移和旋转

1 2	FTransform Mesh2CharInverse = StartChacterFootTransform.GetRelativeTransform(MeshTransformWS); const FTransform ActorTransformWS = Mesh2CharInverse * TargetTransform;

上面的StartChacterFootTransform是角色脚底的Transform，因为RootMotion都是基于脚底的

如果还是不知道如何使用, 可以暴力的记住几个常用场景的用法

Actor本地空间进行旋转和偏移,那么使用左乘变换信息, 即 变换Transform * ActorTransform
在世界空间中进行变换, 那么可以是变换 ActorTransform * 变换Transform

上面的1没什么问题, 对2再进一步解释

比如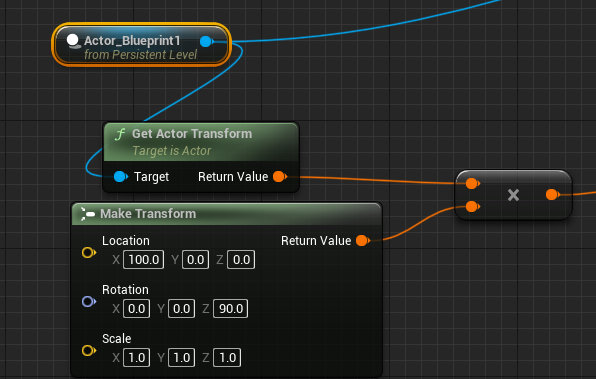

这个几何意义即, 当前这个Actor先绕世界0点进行90度偏移, 然后再基于世界空间的X轴偏移100

上面的操作等价于下图

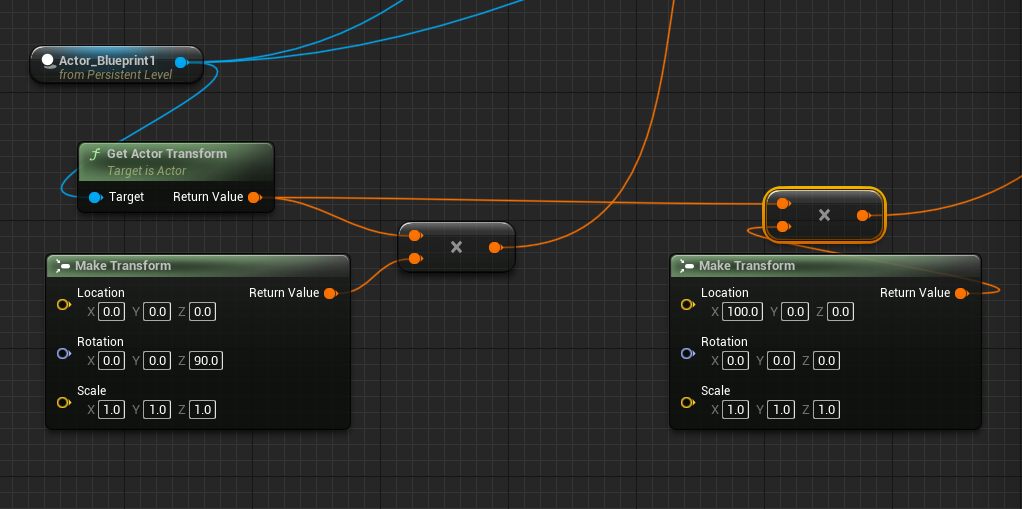
具体的过程如下图

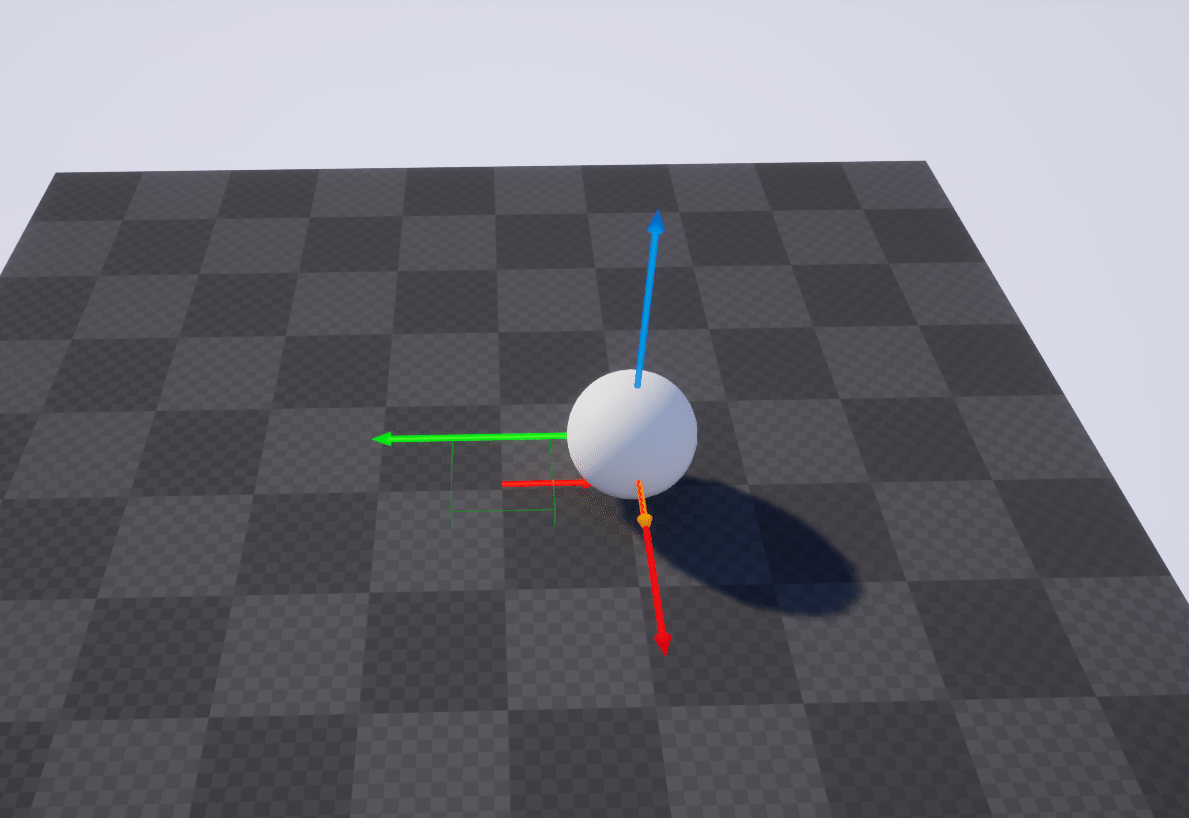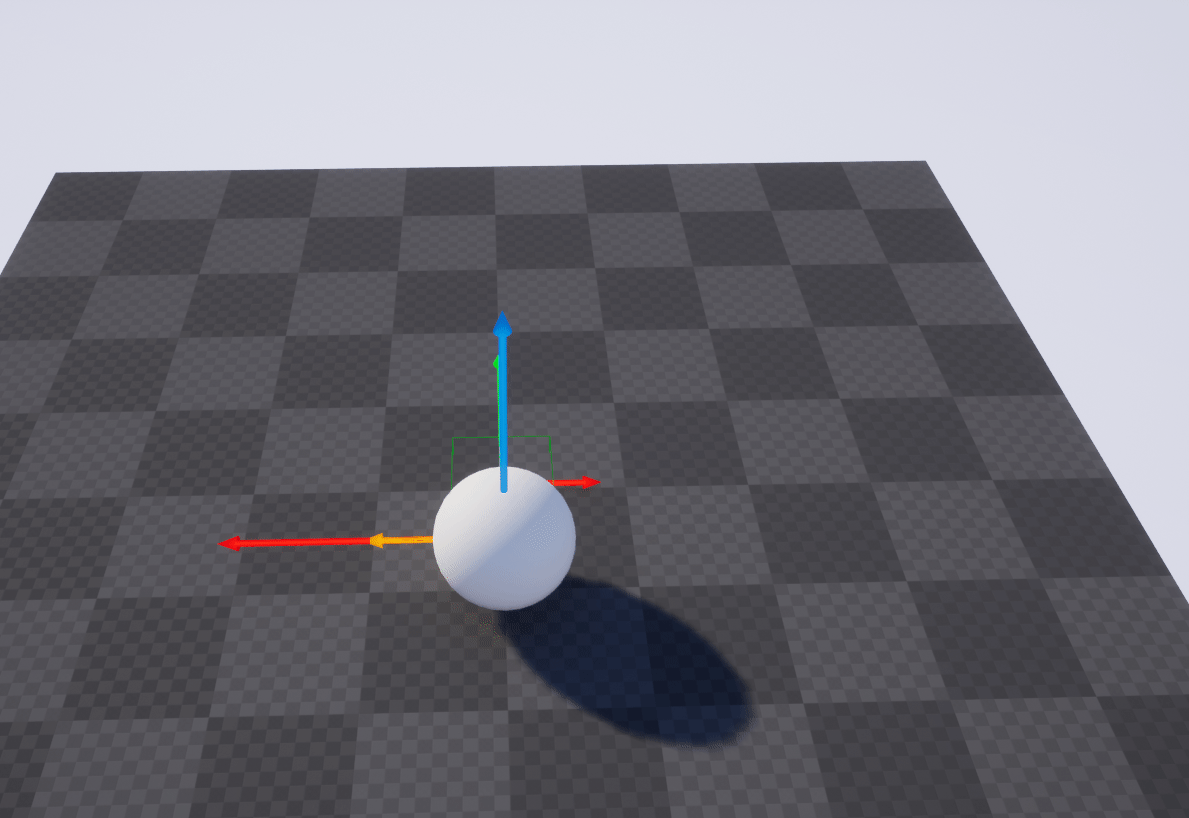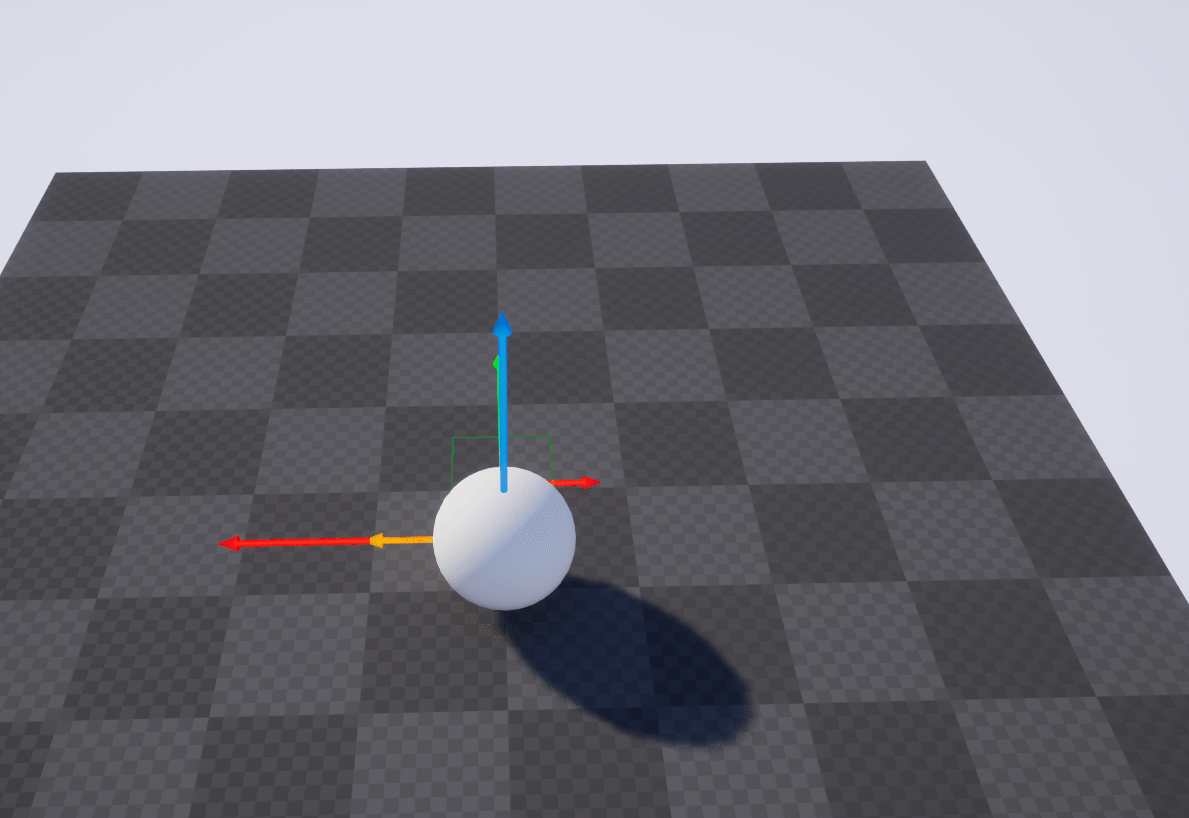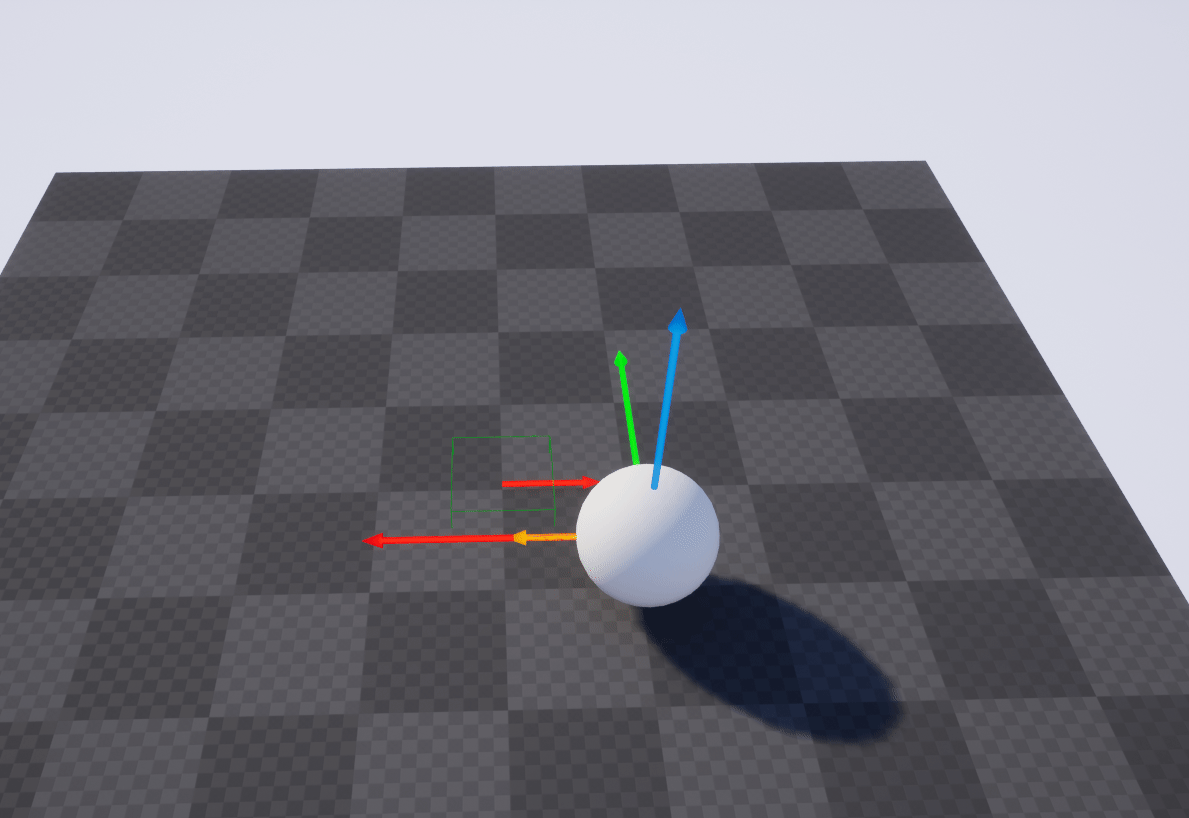
录制_2022_04_11_14_01_20_647

范数

范数是函数，几何意义即比较向量的大小

向量X={2，3，-5，7}

1范数：各个元素的绝对值之和

||X||₁=2+3+5+7=17;

2范数：各个元素的平方和再开更号

||X||₂=(2x2+3x3+5x5+7x7)^1/2=9.3274

p范数：各个向量元素绝对值p次方和的1/p次方
无穷范数：各个元素绝对值最大的哪个元素的绝对值